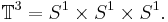Triple torus
Triple torus or three-torus can refer to one of the two following concepts, both related to a torus.
Contents |
Three-dimensional torus
The three-dimensional torus, or triple torus, is defined as the Cartesian product of three circles,
In contrast, the usual torus is the Cartesian product of two circles only.
The triple torus is a three-dimensional compact manifold with no boundary. It can be obtained by gluing the three pairs of opposite faces of a cube. (After gluing the first pair of opposite faces the cube looks like a thick washer, after gluing the second pair — the flat faces of the washer — it looks like a hollow torus, the last gluing — the inner surface of the hollow torus to the outer surface — is physically impossible in three-dimensional space so it has to happen in four dimensions.)
Torus-like surface with three holes
In the theory of surfaces, a triple torus refers to a smooth closed surface with three holes, or, in other words, a surface of genus three. It can be obtained by attaching three handles to a sphere or by gluing (taking the connected sum) of three tori.
See also
External links
- Weisstein, Eric W., "Triple Torus" from MathWorld.